L’analyseur Coradi est une machine entièrement mécanique qui permet de calculer les coefficients du développement en séries de Fourier d’une fonction.

Un exemplaire en est conservé au mus'X. Dans le cadre du cours d'Histoire des sciences et techniques de Frédéric Brechenmacher, une modélisation en 3D en a été faite, ainsi qu'une reproduction de l'appareil.

Très utile avant le développement des calculateurs informatiques, il servait par exemple pour la prédiction des marées en extrayant des mesures de hauteur d’eau la transformée de Fourier.

Ce modèle a connu de nombreuses modifications et améliorations au fur et à mesure de l’avancée de la fabrication.

Les pièces blanches en plastique ont été imprimées en 3D tandis que les pièces transparentes en plexiglas ont été découpées au laser.

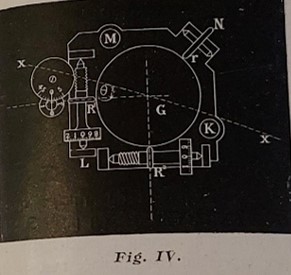
Le cœur du mécanisme de l’analyseur harmonique est l’appareil d’intégration ci-dessous.

Son fonctionnement repose sur la boule centrale (une boule de verre polie dans la machine originale, une boule de billard dans la reproduction).

Lorsque celle-ci est mise en rotation dans une direction quelconque, elle entraine les deux pivots R1 et R2.

Ces pivots font tourner une aiguille qui affiche alors le coefficient du développement en série de Fourier pour une certaine fréquence.

Cette vidéo montre la mise en œuvre de l’analyseur Coradi avec la reproduction.

Le technicien déplace la machine afin que le pointeur suive le tracé de la fonction dont on veut obtenir le développement en séries de Fourier.

La présence de deux pivots (aiguille rouge et verte) permet d’obtenir simultanément le coefficient pour le cosinus et celui pour le sinus.

En effet, on peut voir les fonctions cosinus et sinus comme respectivement l’abscisse et l’ordonnée d’un point en rotation sur un disque. Ici, de part le positionnement perpendiculaire des deux pivots, on retrouve cette même décomposition.

Cette vidéo montre le fonctionnement de l’appareil d’intégration seul. On voit comment la rotation de la boule entraîne les deux pivots.

De plus, suivant la direction de la rotation de la boule, on remarque que les deux pivots ne tournent pas à la même vitesse (il est même possible qu’un des deux pivots ne tournent pas du tout).

Dans la reproduction il a été choisi de ne pas mettre d’échelle comme dans le véritable analyseur Coradi ; l'objectif du travail étant en effet d’expliquer le mécanisme et non de réaliser une reproduction fonctionnelle de la machine.

Dans l’analyseur Coradi complet, la boule de l’appareil d’intégration est mise en rotation par une roue elle-même entraînée directement par le déplacement de la machine. Ainsi, d’un point de vue extérieur, la boule tourne toujours dans la même direction mais dans un sens et avec une vitesse différente suivant la fonction suivie.

Le second contrôle de l’appareil d’intégration est assuré par un système de courroie (un simple fil dans l’analyseur Coradi original). Suivant la position du pointeur sur l’axe des abscisses, la courroie entraîne un engrenage qui fait tourner l’appareil d’intégration. C’est cette rotation qui change la direction de rotation de la boule du point de vue de l’appareil d’intégration. Mathématiquement, c’est ce mécanisme qui réalise la multiplication :

f(x)  cos⁡(nx)

et

f(x)  sin⁡(nx)

.

La fréquence étudiée dépend uniquement de la taille de l’engrenage utilisé : pour calculer le coefficient pour une autre fréquence, il faut changer l’engrenage.

On peut observer ici les deux mécanismes séparément. On voit que seul le déplacement vertical du pointeur (suivant l’axe des ordonnées d’une fonction à étudier) entraîne la boule en rotation, tandis que le déplacement horizontal (suivant l’axe des abscisses) fait tourner l’appareil d’intégration. Ce fonctionnement conjoint, réalisé sur tout le tracé de la fonction, réalise alors l’opération mathématique voulue et donne les valeurs des coefficients an et bn.

par Aurélien Genin (X2021)